Seek in the Dark: Reasoning via Test-Time Instance-Level Policy Gradient in Latent Space

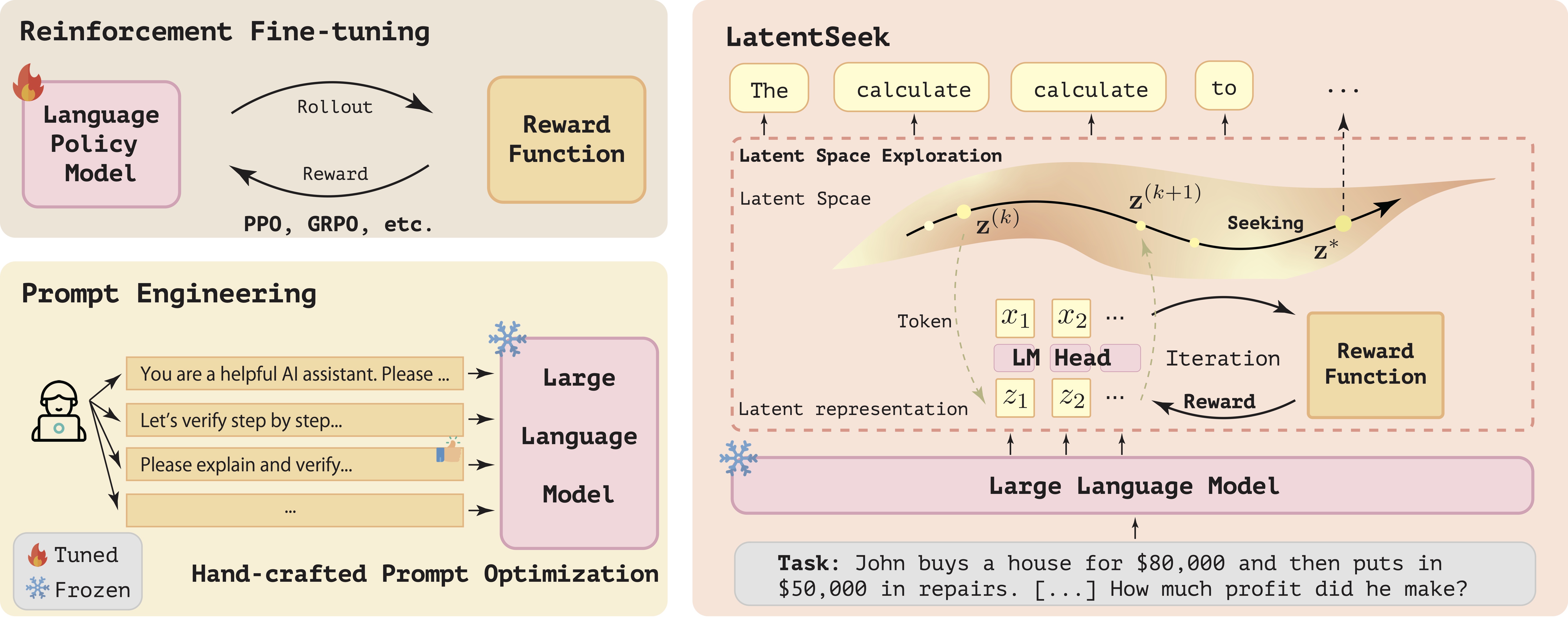
Introduction

Reasoning ability, a core component of human intelligence, continues to pose a significant challenge for Large Language Models (LLMs) in the pursuit of AGI. Although model performance has improved under the training scaling law, significant challenges remain, particularly with respect to training algorithms—such as catastrophic forgetting—and the limited availability of novel training data. As an alternative, test-time scaling enhances reasoning performance by increasing test-time computation without parameter updating. Unlike prior methods in this paradigm focused on token space, we propose leveraging latent space for more effective reasoning and better adherence to the test-time scaling law.
The introduced framework, named LatentSeek, enhances LLM reasoning through Test Time Instance-level Adaptation (TTIA) within the model’s latent space. The latent representations are optimized during the test time using the policy gradient method, to maximize the expected reward. These optimized representations are subsequently decoded into token sequences, which are utilized to compute a new reward, which are then used to guide the next iteration.

TTIA in Latent Space

Given a reasoning problem instance \(\mathbf{c}\) as a context prompt, a pre-trained auto-regressive language model \(\pi\), a reasoning token sequence \(\mathbf{x} = (x\_1, x\_2, \ldots, x\_T)\), and denote the corresponding sequence of latent representations of \(\mathbf{x}\) as \(\mathbf{z} = (z\_1, z\_2, z\_3, \ldots, z\_T)\), the objective is:

where \(R(\mathbf{x}, \mathbf{c})\) is the reward function.

Test-Time Optimization of Latent Representations

Assuming the independence of the latent representations, the test-time optimization is:

and the gradient is calculated as follows:

where \(t\) denotes the position of the latent representation.

LatentSeek Algorithm

The LatentSeek algorithm is described in Algorithm 1. This algorithm iteratively refines the latent representations based on the rewards of generated reasoning paths, effectively performing a guided search through the reasoning space specific to the given problem instance. After each refinement step, the latent representations are decoded into tokens to calculate a reward signal. This signal is then employed to direct the search process in the subsequent iteration. Along with the reward signal, the final output \(\tilde{\mathbf{x}}\) is also explicitly provided. The process runs for a small number of iterations (typically 2-10), stopping early if the reward exceeds a threshold.

Experiments

Results

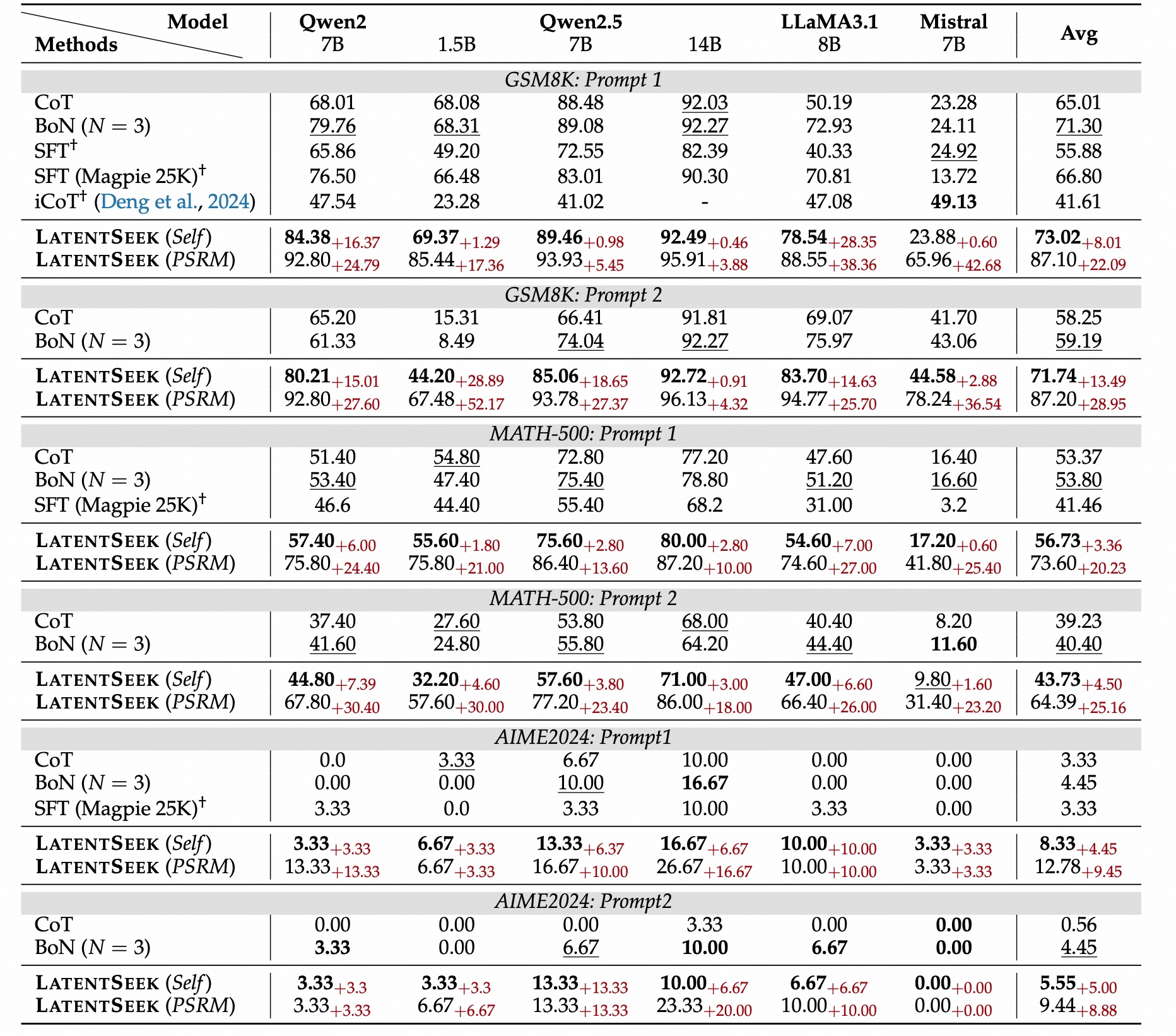
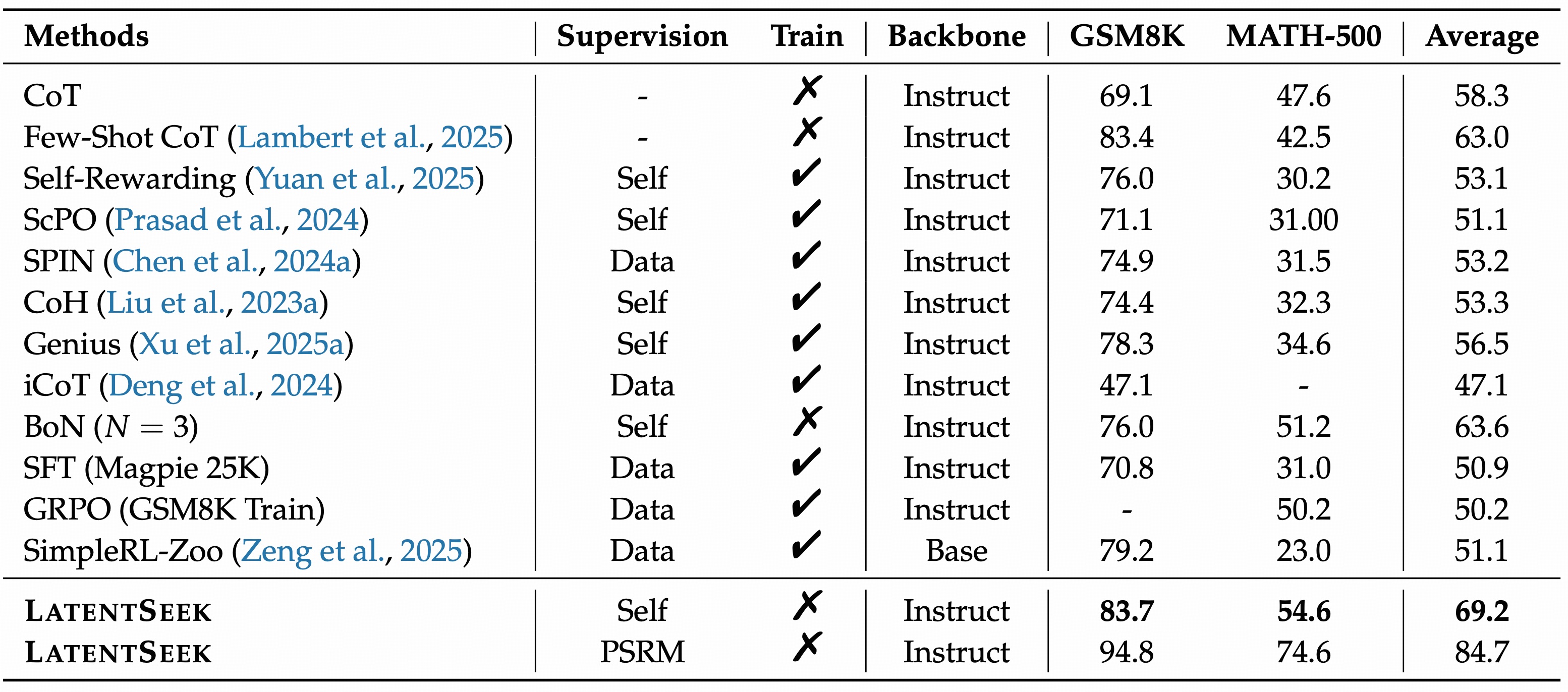
Work or Not: Is Latent Space Powerful Enough?

1. Best Performance on GSM8K, MATH-500: As demonstrated in Table 2, our method outperforms all baseline approaches across all GSM8K, and MATH-500 datasets.
2. Superior Performance on Complex Problems: As shown in Table 1, our approach consistently outperforms all baselines, achieving an average improvement of 4.73% points over CoT across all model families and prompt configurations.
3. Generalizable across backbones: LatentSeek demonstrates superior performance across multiple model families. Also, in terms of model scales, our method consistently outperforms all baseline models across diverse datasets and prompt types
4. Generalizable across prompts: The Qwen2.5 series was explicitly trained using Prompt 1; nevertheless, our methods still achieve notable performance gains.
5. The large potential of LatentSeek, even when guided by sparse reward: when using PSRM, LatentSeek achieves an average improvement of 19.12% score over the CoT method and surpasses the self-reward version by an average of 12.57% score.

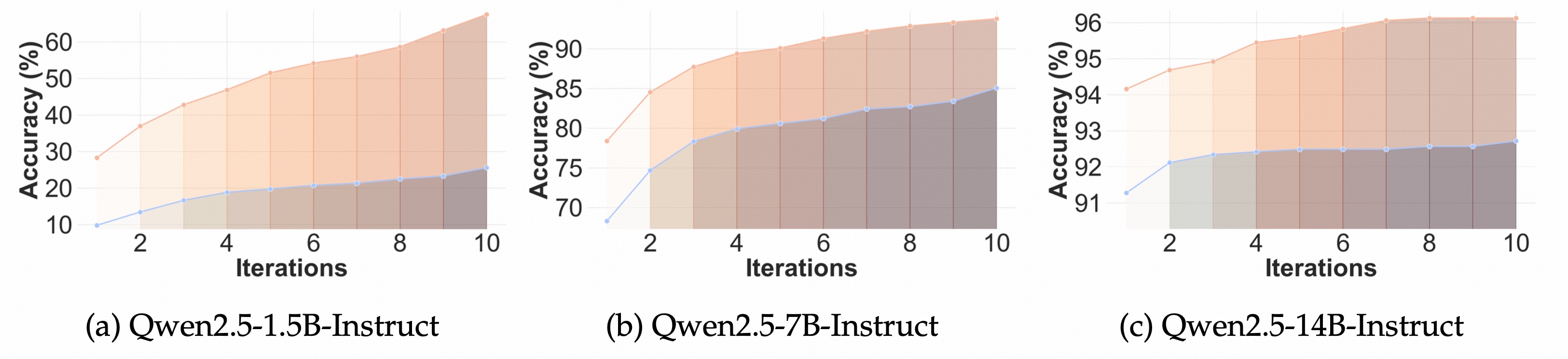
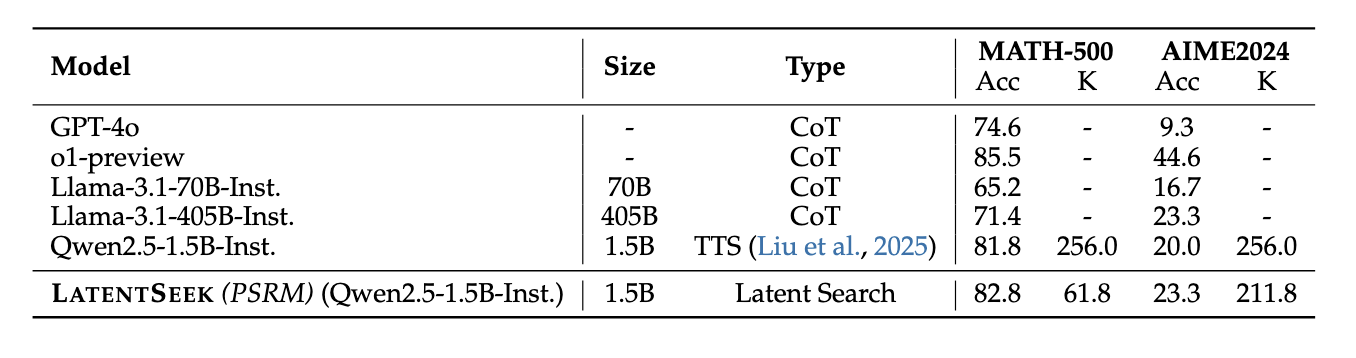
A dream of AGI: Can it be a method for Test-Time Scaling?

1. Test-time scaling can be achieved without necessitating a dense reward function in our setting. (Figure 2)
2. Searching through the latent space offers a promising new direction for test-time scaling. (Figure 2)
3. The latent space represents a more efficient option for test-time scaling compared to the explicit space. (Figure 3)

BibTex

@misc{li2025seekdarkreasoningtesttime,
      title={Seek in the Dark: Reasoning via Test-Time Instance-Level Policy Gradient in Latent Space}, 
      author={Hengli Li and Chenxi Li and Tong Wu and Xuekai Zhu and Yuxuan Wang and Zhaoxin Yu and Eric Hanchen Jiang and Song-Chun Zhu and Zixia Jia and Ying Nian Wu and Zilong Zheng},
      year={2025},
      eprint={2505.13308},
      archivePrefix={arXiv},
      primaryClass={cs.LG},
      url={https://arxiv.org/abs/2505.13308}, 
}